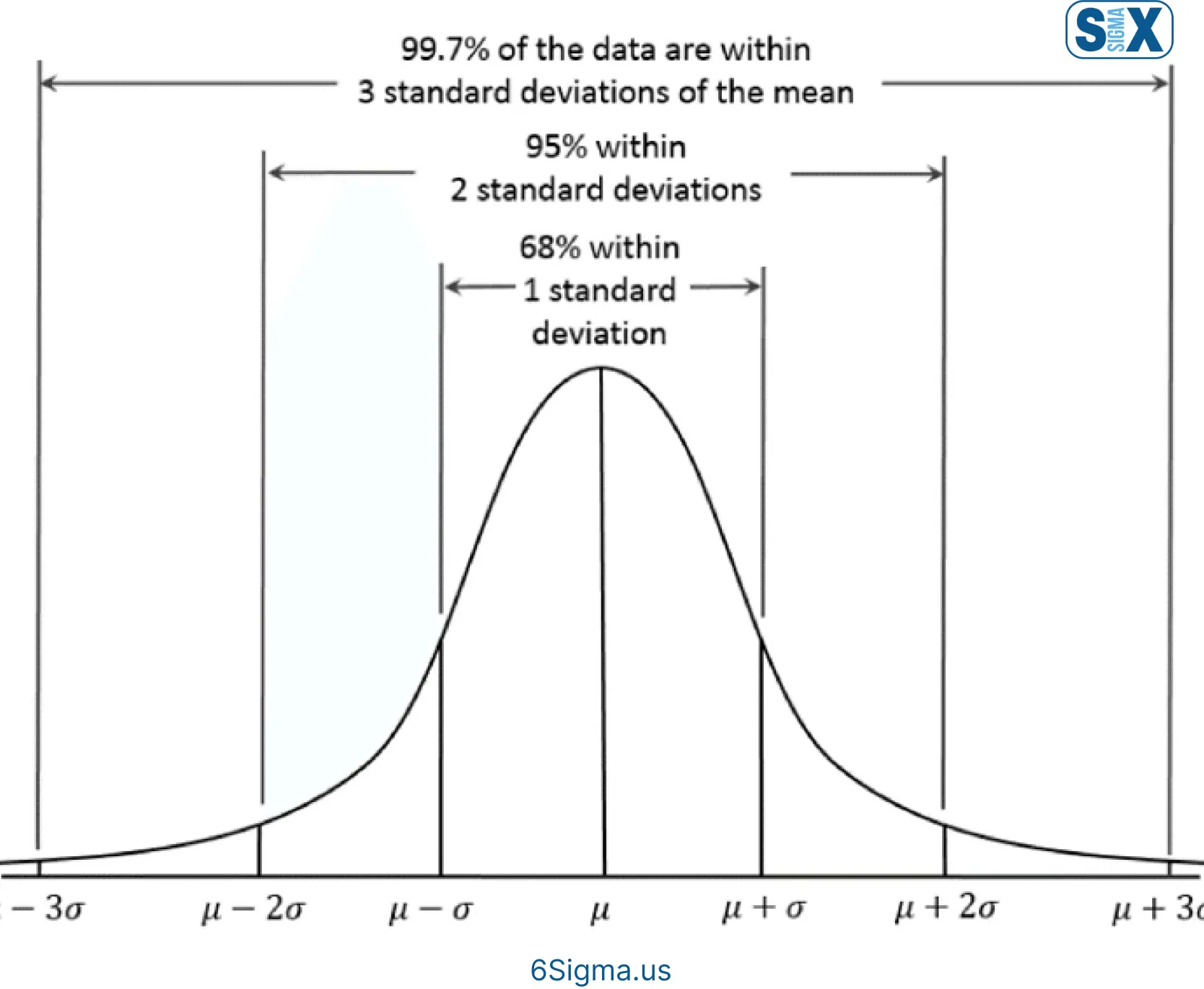
The pooled standard deviation is an important statistical measure used to summarize and describe the amount of variability in a dataset that combines multiple samples or groups. 

Unlike a regular standard deviation calculated on a single sample, the pooled standard deviation allows you to merge and blend the spread of separate groups into one overall estimate of variability.

This enables simplified statistical analysis when comparing groups, testing hypotheses, determining confidence intervals, and more. By pooling the standard deviation, you can get an integrated measure rather than having to analyze each group separately.

The calculation assumes that the variance within each group is similar. So testing this assumption is an important prerequisite before pooling standard deviations.

What is Pooled Standard Deviation?

Pooled standard deviation is a statistical measure of dispersion obtained by combining or pooling multiple sample data sets into one large data set to calculate a standard deviation that is more representative of the overall population. 

The pooled standard deviation is the square root of the pooled variance. In simple terms, it is a weighted average of the individual standard deviations of multiple sample sets.

Mathematically, it is calculated by taking a weighted sum of the variances of the individual samples and then taking the square root of that sum.

Purpose and Applications of Pooled Standard Deviation

The main purpose of using pooled standard deviation is to estimate a more accurate overall variability when dealing with multiple small samples from the same or related total populations. 

Some key applications and use cases of Pooled SD include:

• Combining data from multiple small experiments or trials done under similar conditions to obtain an aggregated measure of dispersion. This allows for making inferences about the overall population.
• In meta-analysis studies where results from multiple independent studies need to be combined and analyzed as one large set.
• In ANOVA testing when comparing variances across different groups or conditions. A pooled standard deviation allows for making a better estimate of the overall variance.
• In statistical process control to monitor processes over time by combining subgroups to obtain control limits.

Explore Pooled Standard Deviation and statistical analysis techniques. With a short course on Introduction to Statistics and Graphical Analysis get a comprehensive foundation for understanding and applying various statistical measures.

Pooled standard deviation gives a better population parameter estimate and allows more powerful statistical analysis when working with multiple small samples.

Calculating Pooled Standard Deviation

The pooled standard deviation is calculated by combining the standard deviations of two or more samples or populations. The main assumptions when calculating a Pooled SD are:

• The samples are independent and randomly selected from their respective populations
• The populations being combined have a normal distribution
• The populations have equal/homogeneous variances

Step-by-Step Method

The formula for calculating the pooled standard deviation is:

s_pooled = √((n_1 – 1)s_1^2 + (n_2 – 1)s_2^2 + … + (n_k – 1)s_k^2) / (n_1 + n_2 + … + n_k – k)

Where:

s_pooled = Pooled standard deviation
s_1 = Standard deviation of sample 1 
s_2 = Standard deviation of sample 2

n_1 = Size of sample 1
n_2 = Size of sample 2 

And so on for additional samples. 

The steps are:

1. Calculate the standard deviation (s) of each sample
2. Square each standard deviation 
3. Multiply each squared standard deviation by its degrees of freedom (n – 1)
4. Sum all the weighted squared standard deviations
5. Divide the sum by the total degrees of freedom of all samples combined
6. Take the square root to obtain the final pooled standard deviation

Example Calculation 

Sample 1 has n_1 = 10, s_1 = 5 

Sample 2 has n_2 = 15, s_2 = 3

s_pooled = √((10 – 1) * (5)^2 + (15 – 1) * (3)^2) / (10 + 15 – 2) 

     = √(9 * 25 + 14 * 9) / 23

     = √(225 + 126) / 23

     = √351 / 23 = 3.79

So the pooled standard deviation is 3.79.

Apply Pooled Standard Deviation calculations and other statistical techniques using industry-standard software. Our Introduction to Statistics and Graphical Analysis with Minitab course offers hands-on training in statistical analysis tools.

Comparison to Regular Standard Deviation

The pooled standard deviation is related to but distinct from the regular standard deviation. While both measure statistical dispersion, they are used in different situations.

Key differences

• The pooled standard deviation combines standard deviations calculated from multiple samples or groups into one overall standard deviation.
  
  The regular standard deviation measures dispersion within a single sample or group.
  
• Pooled SD uses a weighted average based on degrees of freedom. Regular standard deviation takes the square root of the average of squared deviations from the mean.
  
• Pooled SD makes assumptions about the homogeneity of variance across groups. The regular standard deviation has no such assumptions.

When to use Pooled Standard Deviation

• When you have multiple samples and want to determine the overall dispersion for the combined data rather than individual groups. For example, we are comparing test performance across schools.
• It is testing hypotheses that rely on assumptions about homogeneity of variance across groups, like in ANOVA analysis.
• Meta-analyses combine results across many smaller studies to determine an overall effect.

Pooled standard deviation considers variance across multiple groups, while regular standard deviation examines variance within a single group.

The pooled approach is useful for combining data sources and testing assumptions.

Lean Six Sigma in Pooled Standard Deviation

A statistical measure that aggregates variability from multiple samples to generate a more accurate measure of overall dispersion.

Key topics discussed include:

• Definition and Calculation: Pooled SD combines standard deviations from several samples, assuming homogeneity of variance and normal distribution.
• Applications: It has essential uses in various statistical analyses such as ANOVA, meta-analysis, and statistical process control, providing a consolidated estimate of variability.
• Comparison to Regular/Standard Deviation: The article explains how Pooled SD differs from regular standard deviation and outlines scenarios in which each should be used.
• Methodological Considerations: It covers assumptions for pooling, methods for testing variance homogeneity, and alternative robust statistical techniques.

Relevance to Lean Six Sigma

Statistical Foundations

1. Data Analysis and Interpretation: Lean Six Sigma emphasizes the importance of data-driven decision-making. Understanding pooled standard deviation enriches practitioners’ ability to analyze process variability effectively, contributing to better insights in process improvements.
2. Hypothesis Testing in ANOVA: Lean Six Sigma projects often involve comparing groups to identify areas for improvement (e.g., testing different processes for efficiency). The use of pooled SD aligns directly with the analysis phase in DMAIC (Define, Measure, Analyze, Improve, Control), where comparisons across different processes or groups are necessary.

Process Control

1. Statistical Process Control (SPC): The article highlights that pooled standard deviation is vital in SPC, which is a central component of Lean Six Sigma methodologies. SPC utilizes control charts that rely on pooled SD to monitor variations in processes, ensuring that operations remain within desired limits.
2. Continuous Improvement: By employing pooled standard deviation to assess process capabilities and variations, Lean Six Sigma teams can make more informed decisions, facilitating a robust continuous improvement culture.

Custom Sections Derived from Article Themes

Implementing pooled SD in Lean Six Sigma initiatives can streamline data from various trials or tests.

For example, teams can take results from multiple pilot projects, calculate a pooled SD to inform their analysis, and make trade-offs based on a comprehensive understanding of variability.

Meta-Analytic Approaches in Lean Six Sigma

In Lean Six Sigma, especially in multifaceted projects that operate across different functions or departments, the insights from pooled SD facilitate meta-analysis of diverse projects to gauge overall performance improvements and efficiencies.

This aligns perfectly with Lean Six Sigma’s emphasis on systematic data collection and evaluation.

Statistical Practices to Mitigate Risks

When applying Lean Six Sigma, practitioners often work with imperfect data sets, which may violate assumptions of normality and variance homogeneity.

By incorporating robust statistical methods, as discussed in the article, they can ensure that their analyses remain valid even in less-than-ideal conditions.

Examples in Lean Six Sigma Projects

1. Manufacturing Process Improvement: In a production line setting, implementing pooled standard deviation enabled a Lean Six Sigma team to aggregate defect data across multiple shifts. This allowed them to establish more realistic control limits based on pooled variability, ultimately streamlining operations and reducing waste.
2. Healthcare Performance Metrics: In a healthcare organization, a Lean Six Sigma team pooled standard deviations of patient lengths of stay across various departments. This analysis helped to identify which departments had greater variability, leading to targeted process improvements that enhanced patient flow and minimized bottlenecks.

Challenges and Opportunities

Challenges

• Assumption Testing: One of the main challenges Lean Six Sigma practitioners face when harnessing pooled SD is ensuring the homogeneity of variances. If this assumption is violated, it can result in misleading conclusions.

Opportunities

• Enhanced data integration: Combining data sets for a unified analysis can provide Lean Six Sigma teams with a more holistic understanding of process variations.

Practical Advice

• Conduct Homogeneity of Variance Tests: Before using pooled SD, Lean Six Sigma teams should perform Levene’s, Bartlett’s, or Hartley’s tests to confirm variance equality. This can prevent analysis errors stemming from incorrect assumptions.
• Leverage Training: Practitioners should pursue training in both statistical analysis and software tools, such as Minitab, to effectively apply pooled SD techniques in their Lean Six Sigma projects.

Key Takeaways for Lean Six Sigma Practitioners

• Pooled standard deviation is crucial in evaluating variability across multiple samples in Lean Six Sigma projects.
• It aligns with key methodologies, particularly in statistical analysis, hypothesis testing, and process control.
• Practitioners should ensure valid assumptions, leverage robust statistical techniques, and utilize pooled SD for informed decision-making in process improvements.
• Continuous education and training on statistical methods can empower teams to harness data effectively, driving more successful outcomes in Lean Six Sigma initiatives.

Advanced Methods and Considerations

While the basic pooled standard deviation calculation makes some key assumptions, there are more advanced methods available when those assumptions do not hold.

Specifically, there are some considerations around testing whether the variance of each group being combined is equal, using weighted averages to account for differences in sample sizes, and utilizing robust statistical methods.

Testing Homogeneity of Variances

One key assumption made when pooling standard deviations is that the variance of each group is equal. However, in practice, this may not always be true. There are statistical tests available to check whether this assumption of homogeneity of variances holds:

• Levene’s test: An inferential statistic that assesses the equality of variances for a variable calculated for two or more groups.
• Bartlett’s test: A statistic used to test if k samples have equal variances. More robust when data is non-normal.
• Hartley’s test: A simple F-max test for homogeneity of variance. Easy to calculate but less robust than Levene’s.

If these tests show that the variances differ significantly between groups, the pooled standard deviation may not be appropriate.

Weighted Pooled Standard Deviation 

When sample sizes between groups differ substantially, a weighted average can help account for that discrepancy when pooling standard deviations.

The formula adjusts the contribution of each group’s standard deviation to the overall pooled value based on its sample size.

This helps prevent small sample groups from skewing the overall pooled standard deviation.

Robust Methods

Since the standard deviation and pooled standard deviation are sensitive to outliers, robust methods can be used as an alternative:

• Trimean: Pools the 25th, 50th, and 75th percentiles
• Winsorized standard deviation: Limits extreme values before calculating standard deviation
• Median absolute deviation (MAD): Uses median instead of mean.

These provide pooled estimates of dispersion that are less influenced by outliers.

Apply advanced statistical techniques like Pooled Standard Deviation in real-world process improvement projects. Our Lean Six Sigma Green Belt course prepares you to lead data-driven initiatives using a wide range of statistical tools.

Applications and Use Cases

Pooled standard deviation has several important applications in statistical analysis across various fields. Some of the main use cases are:

ANOVA

Analysis of variance (ANOVA) relies on pooled standard deviation to test if there are significant differences between the means of multiple groups.

By combining the standard deviations of the groups, ANOVA gets an estimate of overall variance in the data.

This pooled standard deviation is then used to calculate the F-statistic to test the null hypothesis that all group means are equal.

In ANOVA, a significant F-value indicates that variances between groups are larger than variances within groups. This suggests real differences exist between the means.

Pooled standard deviation enables this central inference in ANOVA analysis.

Statistical Process Control 

In statistical quality control and process monitoring, Pooled SD provides a baseline estimate of process variation over time.

Control charts tracking metrics like defect rates or production output use the pooled standard deviation of historical data as the benchmark. 

New data points are then assessed against the control limits calculated using the Pooled SD.

Points outside these set limits imply a special-cause variation that needs investigation. Using the pooled standard deviation in this manner allows for detecting shifts from the process’s natural random variation.

Meta-Analysis

Meta-analysis seeks to statistically combine data from multiple independent studies to derive consolidated insights.

Variability between the study designs, methods, and populations can make simple averaging of effect sizes misleading. 

By weighting the effect sizes of each study by the inverse of their variances, meta-analysis produces pooled effect size estimates.

The standard error of this pooled effect size depends on the pooled variance across the studies. So pooled standard deviation enables proper meta-analytic integration and inference.