Standard Deviation vs Variance. A Complete Guide for Data Analysis Professionals
Standard Deviation and Variance are crucial in comprehensive data analysis. It helps achieve actionable data that can further be used to optimize manufacturing processes, assess financial risk, or improve customer satisfaction.
The insights gained from properly utilizing standard deviation and variance prove invaluable.
By the end, you’ll be able to
- Differentiate between standard deviation vs variance
- Calculate both measures with confidence
- Choose the appropriate measure for your specific analysis needs
- Apply these concepts to real-world business scenarios
These skills are essential for professionals pursuing a Six Sigma certification, as they form the foundation of data-driven decision making in process improvement.
What is Standard Deviation and Variance?
It is vital to quantify data dispersion as well as project management, and these concepts are fundamental to quantifying dispersion. Let’s examine these concepts and explore their relevance in real-world applications.
Standard Deviation Explained
Standard deviation tells us what the average distance between each data point and the mean in a dataset is. It is symbolized by s (sigma) for population data and s for sample data.
Key points
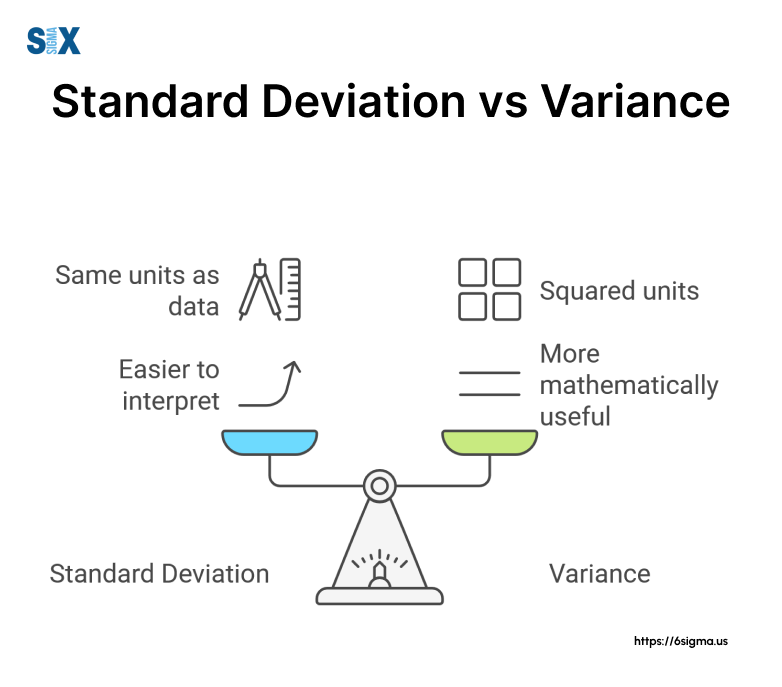
- The standard deviation is the square root of the variance, expressed in the same units.
- Measures the variation present in a dataset.
- Low standard deviation means the data points are closer to the mean, and high standard deviation means the data points are spread out from the mean.
For example, we used the standard deviation for a major automotive manufacturer to monitor the consistency of engine part measurements. A low standard deviation indicated a stable production process, while an increase signaled potential quality issues that required immediate attention.

Curious about how to apply standard deviation in your projects? Our Lean Six Sigma Green Belt course covers this and more.
Variance Explained
Variance, on the other hand, measures the average squared deviation from the mean. It’s denoted as σ² for population data and s² for sample data, Variance provides a more sensitive measure of dispersion, especially when dealing with outliers.
Key points
- Variance is the average of the squared differences from the mean.
- Is used to amplify and quantify the spread of data points, beneficial for identifying extreme variations.
- Plays a fundamental role in statistical tests like ANOVA and regression analysis.
We used variance to analyze customer satisfaction scores during a Six Sigma project for a financial services firm. The high variance in certain service areas highlighted inconsistencies in customer experience, prompting targeted improvements that ultimately led to a 30% increase in customer retention.
Such techniques are fundamental to Six Sigma certification programs, which teach professionals how to leverage statistical analysis for business improvements.
Historical Context
The concepts of standard deviation and variance have rich historical roots in statistical theory:
- Origins: Introduced in the late 19th century by Karl Pearson, a pioneer in mathematical statistics.
- Evolution: Refined through contributions from statisticians like Ronald Fisher, who developed the concept of degrees of freedom.
- Modern applications: These measures have become integral to fields ranging from quality control to machine learning algorithms.
Understanding the historical context helps us appreciate these statistical tools’ robust theoretical foundation. As we continue to push the boundaries of data analysis, these time-tested concepts remain as relevant as ever.
In my experience leading workshops for Fortune 500 companies, I’ve found that professionals who grasp the nuances between a standard deviation vs variance are better equipped to make data-driven decisions. They can more accurately assess risk, optimize processes, and identify opportunities for improvement across various business functions.
The Mathematical Relationship
Now that we’ve established a solid understanding of what a standard deviation vs variance represent, let’s dive into the mathematical relationship between these two crucial statistical measures.
Understanding these formulas and calculations is essential for accurately interpreting data and making informed decisions in various business and project management scenarios.
Formulas Demystified
To truly grasp the relationship between standard deviation and variance, we need to examine their formulas:
Standard Deviation Formula:
σ = √[Σ(x μ)² / N]
Variance Formula:
σ² = Σ(x μ)² / N
Where:
σ = Standard Deviation
σ² = Variance
x = Each value in the dataset
μ = Mean of the dataset
N = Number of values in the dataset
Σ = Sum of
As you can see, the standard deviation is simply the square root of the variance. This relationship is key to understanding how these measures complement each other in statistical analysis.
Step-by-Step Calculation Guide
Let’s walk through the process of calculating variance and deriving standard deviation:
- Calculate the mean (μ) of your dataset.
- Subtract the mean from each data point (x μ).
- Square each of these differences (x μ)².
- Sum up all the squared differences Σ(x μ)².
- Divide the sum by the number of data points (N) to get the variance.
- Take the square root of the variance to obtain the standard deviation.
For example, in a recent Six Sigma project for a manufacturing client, we analyzed the weights of 100 product samples.
By following these steps, we quickly identified that the variance in product weight was 0.25 kg², which translated to a standard deviation of 0.5 kg. This insight allowed us to pinpoint areas of inconsistency in the production process and implement targeted improvements.
Population vs. Sample Considerations
It’s crucial to distinguish between population and sample statistics when calculating standard deviation and variance:
Population: Use N in the denominator of your calculations.
Sample: Use (N-1) in the denominator to account for the degree of freedom lost in estimating the population mean.
In my consulting experience, I’ve found that many professionals overlook this distinction, leading to potentially skewed interpretations of their data. Always clarify whether you’re working with population or sample data before beginning your calculations.

Understanding the mathematical relationship between a standard deviation vs variance empowers you to choose the most appropriate measure for your specific analytical needs.
For instance, when I worked with a financial services firm to optimize their risk assessment models, we primarily used variance to amplify the impact of outliers in investment returns.
However, when communicating these findings to stakeholders, we often converted to standard deviation for easier interpretation in the original units of measurement.
When to Use Standard Deviation vs Variance?
Having explored the mathematical relationship between a standard deviation vs variance, it’s crucial to understand when to apply each measure in real-world scenarios.
As a Six Sigma Master Black Belt, I’ve guided numerous organizations through the process of selecting the most appropriate statistical tool for their specific needs. Let’s dive into the factors that influence this decision and examine some practical applications.
Choosing the Right Measure
When deciding between standard deviation and variance, consider the following factors:
- Unit of measurement: Standard deviation is expressed in the same units as your data, making it more intuitive for direct interpretation.
- Sensitivity to outliers: Variance gives more weight to outliers due to the squaring of differences.
- Analytical purpose: Some statistical tests specifically require variance, while others use standard deviation.
- Communication clarity: Standard deviation is often easier to explain to non-technical stakeholders.
Note: Industry-specific considerations also play a role. For instance, in finance, standard deviation is commonly used to measure investment risk, while in manufacturing, both measures are utilized depending on the specific quality control application.
Standard Deviation Scenarios
Standard deviation is ideal in scenarios where you need to:
- Describe the typical distance from the mean in your original units
- Compare the spread of datasets with different units
- Communicate variability to a general audience
In a recent project with a pharmaceutical company, we used standard deviation to analyze the consistency of active ingredient concentrations in medication batches.
By setting control limits at ±3 standard deviations from the target concentration, we created a robust quality control system that significantly reduced the risk of out-of-specification products reaching consumers.
These statistical process control methods are a key focus of our Six Sigma Green Belt certification and training program.
Variance Applications
Variance is particularly useful when:
- Analyzing the overall spread of data without concern for the original units
- Dealing with datasets where larger deviations are especially important
- Performing certain statistical tests, such as ANOVA or regression analysis
Practical example: While optimizing a call center’s operations, we utilized variance to analyze customer wait times. The higher sensitivity to extreme values helped us identify specific periods or conditions that led to unusually long waits, allowing for targeted improvements in staffing and process flow.
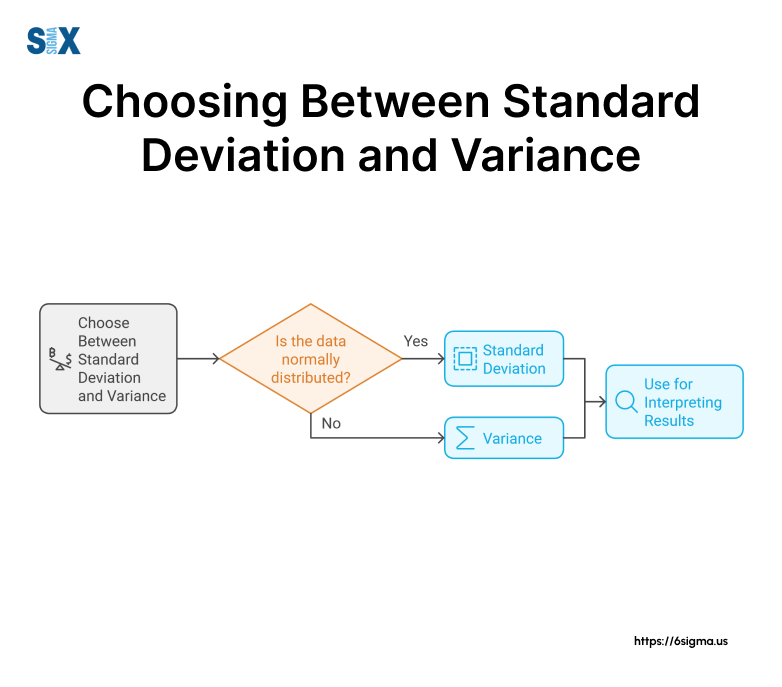
In my experience, one of the most common challenges professionals face is determining which measure to use in a given situation. This decision tree can serve as a quick reference guide to help you make the right choice based on your specific needs and analytical goals.
Remember, the choice between standard deviation and variance isn’t always clear-cut. In many cases, it’s beneficial to calculate and consider both measures to gain a comprehensive understanding of your data’s dispersion.
Applications of Standard Deviation and Variance
As we’ve explored the theoretical foundations of standard deviation and variance, it’s time to examine their practical applications across various industries. Understanding how these statistical measures are utilized in real-world scenarios will help you appreciate their significance in business and project management.
Finance and Investment
In the financial sector, standard deviation and variance are fundamental tools for risk assessment and portfolio management.
Risk Assessment: Standard deviation is widely used to measure the volatility of investment returns. For instance, when I worked with a major investment bank, we used standard deviation to quantify the risk associated with different stocks and mutual funds. A higher standard deviation indicated greater price fluctuations and, consequently, higher risk.
Portfolio Management: Variance plays a critical role in modern portfolio theory. By calculating the covariance between different assets, investors can optimize their portfolios to achieve the best risk-adjusted returns.
In a recent project, we helped a wealth management firm reduce their clients’ portfolio risk by 20% without sacrificing expected returns, all by leveraging variance calculations in their asset allocation strategy.
Quality Control in Manufacturing
The manufacturing industry relies heavily on standard deviation and variance for process capability analysis and Six Sigma applications.
Process Capability Analysis: Standard deviation is used to determine whether a manufacturing process is capable of producing output within specified tolerances.
For a Fortune 500 automotive parts manufacturer, we implemented a process capability analysis using standard deviation, which led to a 40% reduction in defective parts and significant cost savings.
Six Sigma Applications: Both standard deviation and variance are integral to Six Sigma methodologies. In DMAIC (Define, Measure, Analyze, Improve, Control) projects, these measures help identify process variations and verify improvements.
During a recent Six Sigma project for an electronics manufacturer, we used variance analysis to pinpoint the root causes of product failures, resulting in a 60% decrease in warranty claims.
This process of identifying underlying issues is a core component of our root cause analysis training program, which equips professionals with tools to address variability effectively.
Scientific Research
In scientific research, standard deviation and variance are essential for experimental data analysis and calculating margins of error.
Experimental Data Analysis: Researchers use standard deviation to describe the spread of their data and to identify outliers.
When consulting for a pharmaceutical company, we used standard deviation to analyze the efficacy of a new drug across different patient groups, helping to identify which demographics responded best to the treatment.
Margin of Error Calculations: Standard deviation is crucial in determining the margin of error in survey results and experimental findings. This application is particularly important in fields like political polling and market research, where understanding the precision of results is critical for decision-making.
Machine Learning and AI
As we move into the era of big data, standard deviation, and variance continue to play vital roles in machine learning and artificial intelligence applications.
Feature Scaling: In many machine learning algorithms, features need to be scaled to a standard range. Standard deviation is often used in techniques like standardization, which transforms features to have a mean of 0 and a standard deviation of 1.
Model Evaluation: Variance is crucial in assessing model performance, particularly in the context of the bias-variance tradeoff. High variance can indicate overfitting, while low variance might suggest underfitting.
In a recent AI project for a tech startup, we used variance analysis to optimize their recommendation algorithm, resulting in a 25% improvement in prediction accuracy.
Case Study Challenge
A retail company wants to optimize its inventory management. They have collected data on daily sales for various products over the past year. How would you use standard deviation and variance to help them improve their stock levels and reduce waste?
Ready to apply these concepts in real-world scenarios? Our Lean Six Sigma Black Belt program offers advanced training in statistical analysis.
Common Misconceptions and FAQs
In my years of experience training professionals and consulting for various organizations, I’ve encountered numerous misunderstandings about these statistical measures. Clarifying these points will help you avoid common pitfalls and apply these concepts more effectively in your work.
Clarifying Confusions
Misinterpretations of Measures
- “Standard deviation and variance measure the same thing.”
While related, they serve different purposes. Standard deviation measures spread in the original units, while variance uses squared units, making it more sensitive to outliers. - “A low standard deviation always indicates good performance.”
Not necessarily. The desirability of a low or high standard deviation depends on the context. In some cases, like investment returns, higher variability might be preferred for greater potential gains.
Calculation Errors to Avoid
- Using the wrong formula for population vs. sample calculations.
- Forgetting to square the differences when calculating variance.
- Not taking the square root when deriving standard deviation from variance.
In a recent Six Sigma project for a healthcare provider, we discovered that their quality control team had been using the population formula for sample data, leading to underestimated variability in patient wait times. Correcting this error allowed for more accurate process improvement targets.
Frequently Asked Questions
Standard deviation measures the average distance of data points from the mean in the original units of the data variance measures the average squared distance, resulting in squared units.
To convert standard deviation to variance, simply square the standard deviation. Conversely, to get the standard deviation from the variance, take the square root of the variance.
Neither is inherently more important. The choice depends on the specific analysis needs. Variance is often used in advanced statistical procedures, while standard deviation is more intuitive for general interpretation.
Variance is the square of the standard deviation. Mathematically, Variance = (Standard Deviation)².
By addressing these common misconceptions and questions, we aim to solidify your understanding of and the differences b/w a standard deviation vs variance. Remember, mastering these concepts is not just about knowing the formulas, but understanding when and how to apply them effectively in real-world scenarios.
More Concepts and Future Trends
The evolving landscape of data analysis presents new challenges and opportunities for leveraging these fundamental statistical measures. Let’s examine how standard deviation and variance are adapting to meet the demands of big data, machine learning, and quantitative finance.
Standard Deviation and Variance in Big Data
The era of big data has brought scalability challenges to traditional methods of calculating standard deviation and variance. As datasets grow exponentially, efficient computation becomes critical.
Scalability Challenges
- Processing massive volumes of data in real-time
- Maintaining accuracy while reducing computational complexity
Emerging Solutions
- Streaming algorithms for online variance calculation
- Distributed computing frameworks for parallel processing
In a recent project for a major e-commerce platform, we implemented a streaming variance algorithm that reduced computation time by 75% while handling millions of transactions daily. This allowed for real-time anomaly detection in user behavior, significantly improving fraud prevention measures.
Integration with Machine Learning
Machine learning models heavily rely on standard deviation and variance for feature engineering and model optimization.
Feature Engineering Applications
- Normalization and standardization of input features
- Variance thresholding for feature selection
Model Optimization Techniques
- Cross-validation strategies based on variance reduction
- Ensemble methods leveraging variance to improve prediction accuracy
During a machine learning project for a healthcare provider, we used variance-based feature selection to identify the most relevant patient data points. This approach not only improved model accuracy by 15% but also reduced data storage requirements, leading to more efficient and interpretable predictive models.
Stay ahead of the curve in data analysis. Our Design for Six Sigma (DFSS) course covers cutting-edge applications of statistical methods.
Quantitative Finance Applications
The financial sector continues to push the boundaries of standard deviation and variance applications, particularly in risk modeling and predictive analytics.
Risk Modeling Advancements
- Conditional Value at Risk (CVaR) calculations
- Tail risk analysis using extreme value theory
Predictive Analytics
- Volatility forecasting in high-frequency trading
- Scenario analysis for stress testing
In my work with a leading investment bank, we developed a sophisticated risk model that combined traditional variance measures with machine learning techniques to predict market volatility. This hybrid approach improved risk forecasting accuracy by 30%, enabling more informed trading decisions and better capital allocation.
As we look to the future, the importance of standard deviation and variance in data analysis will only grow. Their integration with advanced technologies and methodologies will continue to provide valuable insights across industries. To stay ahead in your field, consider the following action steps:
- Explore online courses on big data analytics and machine learning to understand how these measures are evolving.
- Experiment with open-source tools that implement advanced variance calculation algorithms.
- Stay updated on research papers discussing novel applications of standard deviation and variance in your industry.
Predictive Poll: Which area do you think will see the most significant advancements in applying standard deviation and variance over the next five years?
- Big Data Analytics
- Machine Learning and AI
- Quantitative Finance
- Another field (please specify)
As data continues to drive decision-making across industries, your ability to apply these statistical measures effectively will be a valuable asset in your professional toolkit.
Practical Tools and Resources
It’s essential to equip you with practical tools and resources to apply these concepts effectively in your work. Having the right tools at your disposal can significantly streamline your workflow and improve the accuracy of your calculations.
Software Comparisons
When it comes to calculating standard deviation and variance, numerous statistical software packages are available. Let’s compare some popular options to help you choose the best fit for your needs.
1. Microsoft Excel
Pros
- Widely accessible and user-friendly
- Built-in functions for standard deviation and variance
- Suitable for basic to intermediate analyses
Cons
- Limited capabilities for large datasets
- Not ideal for advanced statistical modeling
2. R (Open-source statistical software)
Pros
- Powerful and flexible for complex analyses
- Extensive library of statistical functions
- Free and open-source
Cons
- Steeper learning curve for non-programmers
- Requires coding skills for advanced usage
3. SPSS (IBM)
Pros
- User-friendly interface with point-and-click functionality
- Comprehensive suite of statistical tools
- Excellent for social sciences research
Cons
- Expensive for individual users
- Can be overkill for simple analyses
In my consulting work, I’ve found that Excel is often sufficient for many business applications. However, for a recent project with a pharmaceutical company analyzing large-scale clinical trial data, we opted for R due to its superior handling of big datasets and advanced statistical capabilities.
Online Calculators and Simulators
For quick calculations or to verify your work, online tools can be invaluable. Here’s a curated list of reliable resources:
- Calculator.net: Offers a simple, user-friendly interface for calculating standard deviation and variance.
- StatPages.info: Provides a comprehensive set of statistical calculators, including advanced options for different types of variance.
- VassarStats: Features interactive tools for probability distributions, which can help visualize the concepts of standard deviation and variance.
Usage Tips
- Always double-check your data input to ensure accuracy.
- Use these tools to verify manual calculations or software outputs.
- Explore the educational resources often provided alongside these calculators to deepen your understanding.
To master these calculations and their applications, our Six Sigma certification and training programs offer hands-on training with statistical tools and real-world scenarios.
By leveraging these tools and resources, you can enhance your efficiency and accuracy when working with standard deviation and variance. Remember, the key is not just in the calculation itself, but in the interpretation and application of these measures to drive meaningful insights and decisions in your work.
Going Further
Throughout this article, we’ve dissected the fundamental differences between standard deviation vs variance, from their definitions and formulas to their practical applications across various industries.
We’ve seen how these statistical measures serve as powerful tools for quantifying variability, assessing risk, and uncovering valuable insights hidden within datasets.
Key takeaways
- Standard deviation measures spread in the original units of the data, making it more intuitive for interpretation.
- Variance uses squared units, making it more sensitive to outliers and useful in advanced statistical analyses.
- Both measures play critical roles in fields such as finance, manufacturing, scientific research, and machine learning.
- The choice between a standard deviation vs variance depends on the specific context and analytical needs of your project.
Real-world application of these concepts has demonstrated their transformative power. From optimizing investment portfolios to enhancing quality control in manufacturing processes, standard deviation, and variance continue to be indispensable tools in the data analyst’s toolkit.
As a Six Sigma Master Black Belt, I’ve witnessed firsthand how a deep understanding of these measures can drive significant improvements in business processes and decision-making. In one particularly impactful project, we used variance analysis to identify and reduce sources of variability in a pharmaceutical production line, resulting in a 40% decrease in defective products and millions in cost savings.

Remember, mastering the concepts of standard deviation and variance is not just about mathematical proficiency; it’s about developing a keen analytical mindset that can uncover meaningful patterns and drive informed decision-making.
SixSigma.us offers both Live Virtual classes as well as Online Self-Paced training. Most option includes access to the same great Master Black Belt instructors that teach our World Class in-person sessions. Sign-up today!
Virtual Classroom Training Programs Self-Paced Online Training Programs







